Sine meaning delves into the depths of trigonometry, unraveling the intricacies of this fundamental function that has shaped mathematics, science, and engineering for centuries. From its etymological roots to its indispensable role in wave theory and computer graphics, sine’s significance extends far beyond mere mathematical calculations.
In the realm of trigonometry, sine is the ratio of the opposite side to the hypotenuse in a right triangle, forming the cornerstone of triangle solving and navigation. Its applications extend to acoustics, optics, and electromagnetism, providing a framework for understanding periodic motion and modeling real-world phenomena.
Etymology of Sine
The term “sine” originates from the Latin word “sinus”, which means “bay” or “curve”. In ancient geometry, the sine of an angle was defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
This definition was later extended to angles greater than 90 degrees by defining the sine as the ratio of the length of the opposite side to the length of the hypotenuse in a triangle formed by extending one of the legs of the right triangle.
Mathematical Definition of Sine
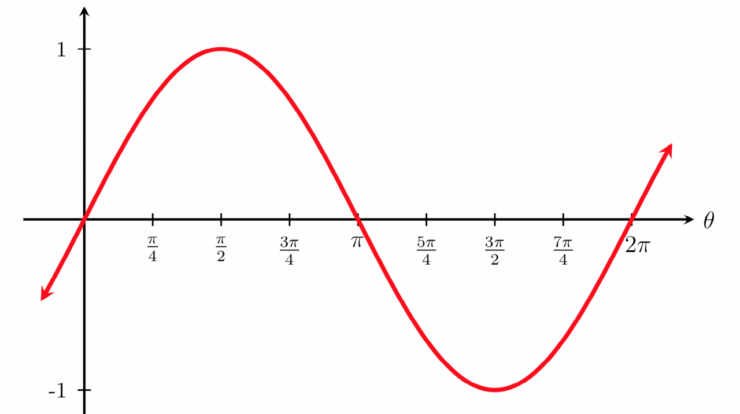
In trigonometry, the sine of an angle is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle. The sine function is a periodic function with a period of 2π. The sine function is also an odd function, meaning that sin(-x) = -sin(x).
The sine function is related to the cosine function by the identity sin 2(x) + cos 2(x) = 1.
Applications of Sine in Trigonometry
The sine function is used to solve triangles. For example, the sine law can be used to find the length of a side of a triangle if the lengths of the other two sides and the measure of one angle are known.
The sine function is also used in navigation, surveying, and engineering.
Sine in Calculus
The derivative of the sine function is the cosine function. The integral of the sine function is the negative cosine function. The sine function is used in Taylor series expansions. The sine function is also used in differential equations and Fourier analysis.
Sine in Physics
The sine function is used to describe periodic motion. For example, the sine function can be used to describe the motion of a pendulum or the vibration of a string. The sine function is also used in acoustics, optics, and electromagnetism.
Sine in Computer Graphics, Sine meaning
The sine function is used to generate curves and surfaces. The sine function is also used in computer animation and modeling. The sine function is used to create realistic effects in digital imagery.
Cultural and Historical Significance of Sine
The sine function has been used in mathematics and astronomy for centuries. The sine function was used by the ancient Greeks to calculate the length of the Earth’s circumference. The sine function was also used by the ancient Egyptians to build the pyramids.
The sine function is still used today in a wide variety of applications.
Final Wrap-Up
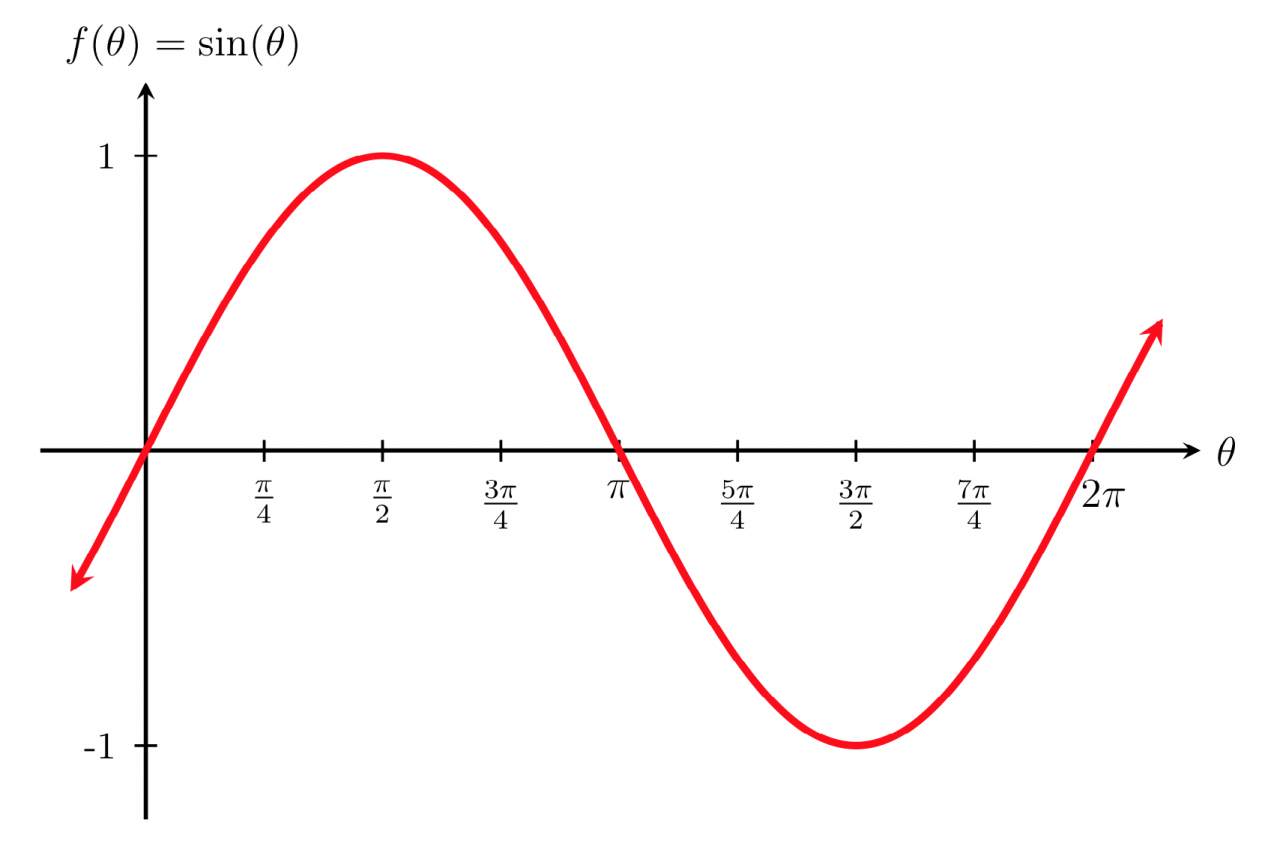
Sine meaning encompasses a rich tapestry of mathematical, scientific, and cultural significance. Its versatility and elegance have made it an indispensable tool for understanding the world around us, from the motion of celestial bodies to the intricate patterns of sound and light.
As we continue to explore the depths of sine, we uncover a function that transcends its mathematical origins, touching upon the very fabric of our universe.
Commonly Asked Questions: Sine Meaning
What is the sine of an angle?
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
How is sine used in navigation?
Sine is used in navigation to calculate the distance between two points on the Earth’s surface.
What is the relationship between sine and cosine?
Sine and cosine are related by the Pythagorean identity: sin²θ + cos²θ = 1.